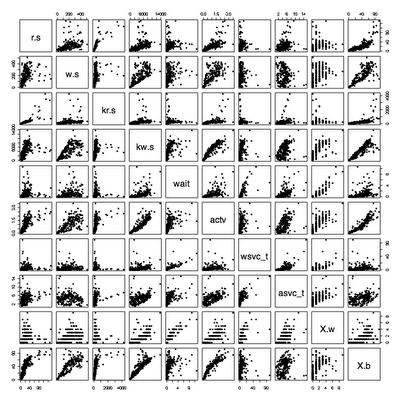
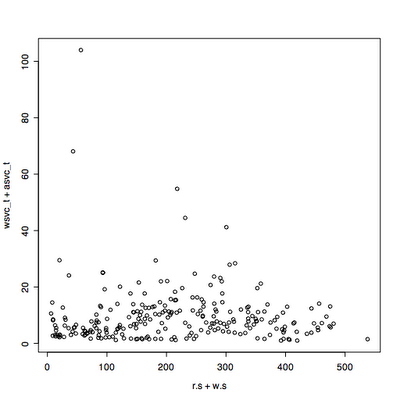
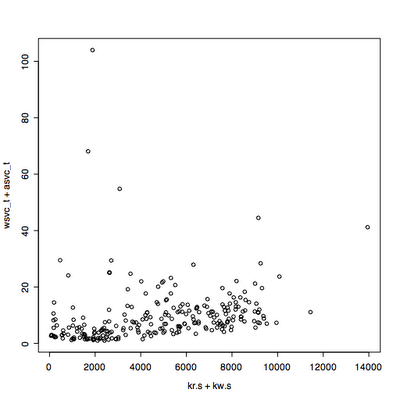
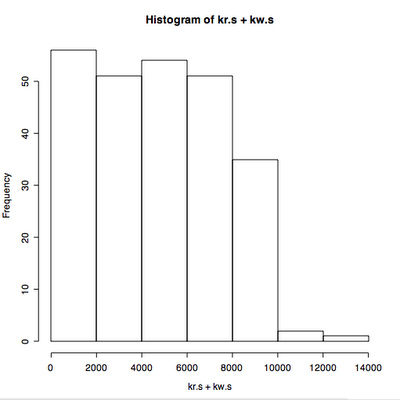
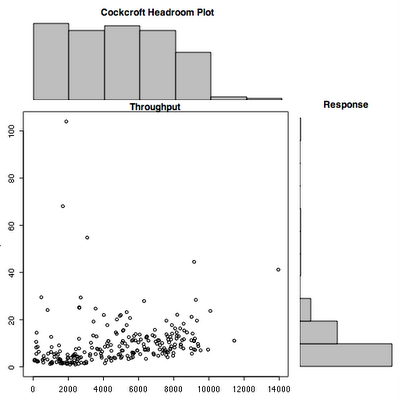
Main changes: the quantile used to remove outliers now only removes outliers that exceed the 95th percentile response time by default. It keeps all the throughput values unless you use qx=True.
In each of the throughput bins used to draw the histogram, the maximum response time for that bin is now calculated and displayed as a staircase line unless you set max=False.
The set of data is now split into ranges and color coded. The times series plot is coded so you can see the split, and the scatterplot shows how those points fall. I have been plotting weekly data at one minute intervals with split=7, which looks pretty good.
I read in some data that has been extracted from vxstat into a csv format at a known URL and plotted it three ways.
I plot the first 2880 data points, picking the read data rather than write, two days at one minute intervals.
> stime <- read.csv(url("http://somewhere/vxstat_response"))
> sops <- read.csv(url("http://somewhere/vxstat_throughput"))
> names(sops)
[1] "DateTime" "vxstat_dg_operationsRead"
[3] "vxstat_dg_operationsWrite"
> chp(sops[1:2880,2],stime[1:2880,2])
> chp(sops[1:2880,2],stime[1:2880,2],q=1.0)
> chp(sops[1:2880,2],stime[1:2880,2],q=1.0,splits=8)



Here is the code that generates the plot.
> chp <-function(throughput,response, q=0.95, qx=F, xl="Throughput",yl="Response",tl="Throughput Over Time",
ml="Headroom Plot", fit=T, max=T, splits=0) {
# remove zero throughput and response values
nonzer <- (throughput != 0) & (response != 0) # array of true/false
y <- response[nonzer]
x <- throughput[nonzer]
# remove outliers, keep response time points inside 95% by default
if (q != 1.0) {
quant <- (y < quantile(y,q))
# optionally trim throughput outliers as well
if (qx) quant <- quant & (x < quantile(x, q))
x <- x[quant]
y <- y[quant]
}
# make histograms and record end points for scaling
xhist <- hist(x,plot=FALSE)
yhist <- hist(y,plot=FALSE)
xbf <- xhist$breaks[1] # first
ybf <- yhist$breaks[1] # first
xbl <- xhist$breaks[length(xhist$breaks)] # last
ybl <- yhist$breaks[length(yhist$breaks)] # last
xcl <- length(xhist$counts) # count length
ycl <- length(yhist$counts) # count length
xrange <- c(0.0,xbl)
yrange <- c(0.0,ybl)
xlen <- length(x)
# make a multi-region layout
nf <- layout(matrix(c(1,3,4,2),2,2,byrow=TRUE), c(3,1), c(1,3), TRUE)
layout.show(nf)
# set plot margins for throughput histogram and plot it
par(mar=c(0,4,3,0))
barplot(xhist$counts, axes=FALSE,
xlim=c(xcl*0.00-xbf/((xbl-xbf)/(xcl-0.5)),xcl*1.00),
ylim=c(0, max(xhist$counts)), space=0, main=ml)
# set plot margins for response histogram and plot it sideways
par(mar=c(5,0,0,1))
barplot(yhist$counts, axes=FALSE, xlim=c(0,max(yhist$counts)),
ylim=c(ycl*0.00-ybf/((ybl-ybf)/(ycl-0.5)),ycl*1.00),
space=0, horiz=TRUE)
# set plot margins for time series plot
par(mar=c(2.5,1.7,3,1))
plot(x, main=tl, cex.axis=0.8, cex.main=0.8, type="S")
if (splits > 0) {
step <- xlen/splits
for(n in 0:(splits-1)) {
lines((1+n*step):min((n+1)*step,xlen), x[(1+n*step):min((n+1)*step,xlen)], col=4+n)
}
}
# set plot margins for main plot area
par(mar=c(5,4,0,0))
plot(x, y, xlim=xrange, ylim=yrange, xlab=xl, ylab=yl, pch=20)
if (max) {
# max curve
b <- xhist$breaks
i <- b[2] - b[1] # interval
maxl <- list(y[b[1] < x & x <= (b[1]+i)])
for(n in b[c(-1,-length(b))]) maxl <- c(maxl,list(y[n < x & x <= (n+i)]))
#print(maxl)
maxv <- unlist(lapply(maxl,max)) # apply max function to elements of list
#print(maxv)
#lines(xhist$mids,maxv,col=2) # join the dots
#staircase plot showing the range for each max response
lines(rep(b,1,each=2)[2:(2*length(maxv)+1)],rep(maxv,1,each=2),col=3)
}
if (fit) {
# fit curve, weighted to predict high throughput
# create persistent chpfit object using <<-
chpfit <- glm(y ~ x, inverse.gaussian, weights=as.numeric(x))
# add fitted values to plot, sorted by throughput
lines(x[order(x)],chpfit$fitted.values[order(x)],col=2)
}
if (splits > 0) {
step <- xlen/splits
for(n in 0:(splits-1)) {
Sys.sleep(1)
points(x[(1+n*step):min((n+1)*step,xlen)],y[(1+n*step):min((n+1)*step,xlen)], xlim=xrange, ylim=yrange, col=4+n)
}
}
}